TALC moved to 9-10:30 am next Tuesday

Next monday (10/31) is Halloween, so we will not have TALC that morning. Instead, we will have TALC from 9-10:30 am on the following Tuesday morning (11/1). The week after that, TALC will continue at the regular time on Monday evenings.

Visitors for Wed and Fri

We'll be joined in class Wednesday by Dr. Ryan Foley (Harvard CfA). Come prepared for a brief Q&A with Ryan at the beginning of class Wed.

On Friday, Dr. Samaya Nissanke will visit us once again and bring a worksheet on GR for us to play around with.

Major Blogging Assignment

One of the main goals of Ay20 as stated on the course website is that, "Students will understand what it means to be a professional astronomer." Jackie and I put a lot of thought into these goals and we fully intend to meet them by the end of term.


Pursuant to this goal, your assignment is to team up with 2-3 of your classmates and put together a series of 3-4 blog entries on the overarching topic of: "What does it take to be a professional astronomer." This topic, as stated, is broad and a bit ill defined by design. Tackle it as you see fit. However, here are some concrete suggestions:

1. Write down your impressions as of right now. What does it take to be a professional astronomer. What is the ultimate goal? What is your goal? This can form the basis of your first post.
2. Interview a grad student and a postdoc, perhaps several. Or interview a junior faculty member, or well-established prof. Write a friendly yet professional email to your prospective interviewee, invite them to lunch or out for an afternoon coffee/tea at the Red Door. The Q&A (questions in bold, responses in normal text) can form the basis of a second blog post. What is the typical career arc of a pro? What is a postdoc? Where did they apply to grad school? Where did they start out as an undergrad? What do they know now that they wish they knew at your age? What are their career aspirations?
3. What are alternative career arcs? What are the prospects in engineering, working at observatories, national labs, or in industry?
4. Find articles on this topic online. Check out the discussions on astrobetter and read the career development posts on astrobites. What have you learned and how has your impression from step 1 changed now that you've researched the topic? This can be your third (or fourth) post.

Share the various tasks (interviewing, reading, writing) among your team members. Meet regularly to compare notes. Use Google Docs to write collaboratively. Talk to Jackie and myself. 

This assignment is due before the end of term, the sooner the better. What ever you do, please do not wait to do this all in one or two nights. Start now! And have fun with it. 

Pics, please!

Please send me your pictures from our Palomar trip. I'd like to compile them into a post here on the course blog.

Thanks!

Monday's Visitor

Monday we'll be joined by Dr. Phil Muirhead, a postdoctoral scholar here in Cahill who is an experimental astrophysicist. Here's his webpage. Check him out and come to class with questions for him.

Spectroscopy

http://xkcd.com/964/

In case you don't get the reference in the first poster on the wall...

Lab 2 deadline moved to Wednesday

In response to feedback from students (which is very helpful!), the lab 2 deadline has been moved to next Wednesday, 10/19.

Reminder: Palomar trip this weekend

Don't forget the Palomar trip is this Sunday, 10/16! We will meet at noon at Cahill (eat lunch beforehand), drive the three hours out to Palomar, and stay there through evening to do a bit of observing/stargazing. You should pack a "night lunch" (dinner) since we will get back late.

Lab 2

Lab 2 has been posted on the course web site: http://www.astro.caltech.edu/~jrv/Ay20/labs/lab2_theAU.pdf. In this lab, you will use an image of Mercury's transit of the Sun, taken by the TRACE mission, to estimate the distance to the Sun. This builds on our measurement of the radius of the Earth (but feel free to use a more accurate value than the one we got). The lab is due Sunday night by midnight.

The Known Universe

Here's the video I showed in class Monday. Enjoy!

Week 3 Reading

Read C&O Chapter 3.3-3.5 (The Nature of light, Black bodies)

iObserve

Right on the heels of our celestial sphere lessons, here's a post at Astrobetter about a handy tool for planning your observations.

Monday's Guest

Monday we'll be joined by an esteemed visitor, Dr. Jon Swift:

http://jonswiftastro.com/

Dr. Swift was my graduate student mentor at UC Berkeley and we both ended up at the University of Hawaii together as postdocs, where he was a Sub-millimeter Array Postdoctoral (SMA) Fellow. His research focus is on massive star formation and he uses interferometers to study molecular clouds where these behemoth baby stars are born.

Dr. Swift is also a professional musician, photographer, poet and an accomplished surfer.

Come prepared with questions for our guest. We'll also be learning about blackbody radiation, so stay tuned for the worksheet, which will be posted this weekend.

Carnegie Observatories Open House

Oct 23, 2-5pm
Santa Barbara St.
Pasadena
http://obs.carnegiescience.edu/Events/openhouse2011

That rock

Here's an example of a mid-level (~3 points) lab/HW writeup. A 5-pointer will go into much more detail.

On the Mass of That Rock

by: John A. Johnson

Abstract


I can't remember numbers very well, but I like to calculate stuff. Here's an example of how using street fighting mathematics can help people with poor memories make order-of-magnitude calculations.


Introduction

Hey, how much does that rock weigh (see Figure 1)? Let's figure it out on the way to lunch at Chandler.

Figure 1: A rock

Solution

Well, we know the density of the rock will be comparable to the average density of the Earth. The density of the Earth depends on the mass and radius of the Earth. I used to have both of these quantities memorized, but the process of learning all the Ay20 students' names forced these constants out of my cache.

From my most recent frequent flyer statement I know that the distance from LA to NY is about 3000 miles, which is 4800 km =~ 5e8 cm. There are about ~5 United Stateses around the globe (maybe 6), and this distance divided by 2pi =~ 6 is the radius of the Earth, or R =~ 5e8 cm.

The acceleration of an object dropped near the surface of the Earth is about 10 m/s^2 or 1000 cm/s^2 (I can remember 10!).

The density is the mass divided by the volume, or ~7 g/cc. That rock is about a meter cubed, or 10^6 cc, so it must contain 7 million grams, or 7 metric tons. That's a lotta rock!

Epilogue

It turns out that the average density of the Earth is more like 5.5 g/cc, and the density of the rock in Figure 1 is likely less than this average value, unless it's solid lead or some such. This table gives the density of various materials in kg/cc. Most surface rock is around 2.5-3.0 g/cc, so I'm off by a factor of 3. Which means I'm dead-on to an order of magnitude!

Acknowledgements

I extend my gratitude the lady with the stroller (not pictured) for jumping out of the way just before I snapped this picture.

Palomar Field Trip

We will have a VIP tour of Palomar Mountain and its facilities Sunday Oct 16. We'll leave from Cahill at 1pm and we'll stay until after sunset (provided that the weather cooperates). Please find someone with a car and reserve your seat. I'll have 3+2 seats available, where the +2 seats are for people under 5'4".

Reading (viewing): Fourier Transforms

First, watch this nice intro to the topic:


Then read Chapter 2 of Gray's Stellar Photospheres. Read enough to understand Figure 2.4 (this was incorrectly labeled as Figure 2.8 in a previous version of this post. Fortunately the hyperlink went to the correct figure.), which you should memorize for life.


We'll think about telescope optics and astronomical instrumentation mostly using 1-d visualizations. As additional reading you can check out this introduction to FT for 2-dimensional functions (images).

Worksheet 2

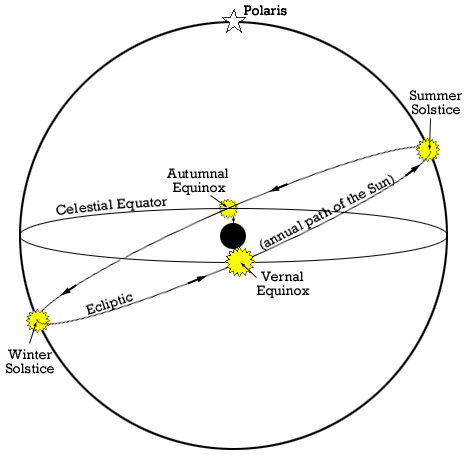
Worksheet 2: The Celestial Sphere and Observation Planning

Note that this was originally going to be assigned Friday, but we'll put it off until Monday. Your group's write up of one or two of these problems is due by next Sunday (Oct 9). There will be a help session Monday evening. Together with your time in class, this gives you about 2.5-3.0 hours to work on the problems.

Also, I'm having trouble with URLs in LaTeX containing characters such as "_" and "~". Here are the Keck targets for you to organize.

http://www.astro.caltech.edu/~johnjohn/outgoing/keck_targets.txt

Estimating The Luminosity of a Sun-like Star

by: John A. Johnson, Jackie Villadsen


Abstract


We present the solution to Worksheet problem #2, from week 1, estimating the power output of a Sun-like star. Each group should submit one to two of these per week. Decide amongst your group members who will be first author, second author, etc. Acknowledge people and resources used in your solution. Cite ancillary information. State your assumptions clearly. Write your solution such that a frosh could duplicate your steps and arrive at the same solution.


Introduction


The oldest astronomical instrument is the human eye. A marvel of evolution, the eye has both high sensitivity and a large dynamic range. A classic study of the eye's response to light conducted in 1942 showed that of order 10 photons need to impinge on the eye in order for the brain to register detection (Hecht, Schlaer & Pirenne 1942). In other words, the eye has a gain of 10 photons/DN. In this contribution we use this fact as a starting point for estimating the luminosity (power output) of a Sun-like star. As additional input for our calculation we note that a Sun-like star at 100 light years is just barely visible to the naked eye if the star is viewed from a dark site. (As a side note, this corresponds to a G2V star with an apparent magnitude of V=6).

Order of Magnitude (OoM) Calculation

We start with a rough estimate of the aperture area of the eye. Fully dilated, an eye has an entrance diameter of roughly Reye = 0.5 cm, corresponding to an area of 0.25 cm^2. From here on we consider only a single eye since it is unclear how two eyes would combine for the detection of a faint star, and since we will only incur a factor-of-two error at most, which is insignificant for our OoM calculation. As an additional assumption we ignore absorption by the Earth's atmosphere and set interstellar reddening to zero.

The star is at a distance of 100 light years. Light travels at 3x10^10 cm/s, and there are (π x 10^7) seconds in a year. A light year is therefore D ~ (10 x 10^10 x 10^7) = 10^18 cm. The star emits some number Nemit photons isotropically, and the eye subtends a tiny fraction of the area of a sphere with a radius of D = 10^20 cm and receives 10 photons. This fractional area is (AD/Aeye), where Aeye is the area of the eye and AD is the area of the sphere surrounding the star. Thus

We are interested in the power output of the star, which is the energy emitted per second. We can get the energy corresponding to Nemit photons with 

where \lambda is the wavelength of light. We can assume that the eye's spectral response is well-tuned to the peak of the Sun's spectral energy distribution, which corresponds to about 550 nm (we'll learn more about this after we estimate the Sun's temperature and learn about black body radiation). Thus

where I have used cgs throughout (note that 550 nm = 550 x 10^-7 cm). Now we need to figure out the time interval. The eye detects the 10 photons at a certain "readout rate." This can be estimated by noting that movies are typically shot at 24 frames per second. At a slower rate the eye would notice a distinct slowing of the movie scenes (imagine watching a movie that shows one frame every second, i.e. a slide show), and at a faster rate the movie studio would be wasting film. So the time the brain takes to "read out" the eye is about 10 milliseconds or 0.01 seconds, to an OoM. Thus, the power output of the Sun-like star is

This compares well to the actual luminosity of the Sun, which is 3.862 x 10^33 ergs/s. 

Summary and Discussion

We have performed an OoM calculation of the Sun's luminosity by noting that a Sun-like star at 100 pc is barely visible to the naked eye. Our final answer is correct to within a factor of 4, demonstrating the usefulness of OoM calculations. By not worrying about the exact numbers, but instead focusing on the problem-solving process, we are free to concentrate on the physics of the problem knowing that we can perform the exact calculation using the same reasoning and a bit more time/effort. 

Acknowledgements


We thank Owen and Marcus Johnson for playing nicely with each other for the 45 minutes it took Daddy to write this. We made use of WolframAlpha when our initial estimate of the photon energy was off by two orders of magnitude, and when we couldn't remember Planck's constant in cgs. WolframAlpha helped us realize that we needed the wavelength of a green photon in cm rather than meters. Duh. The equations were generated using CodeCogs online LaTeX editor.

On the Earth's radius, the beach, and balance

I hope you all enjoyed this lab as much as I did. We may or may not get an accurate measurement of the Earth's radius. However, either way, we had an opportunity to get to know each other better, which will no doubt help us work collaboratively and learn more from the class. 

On the way back to Pasadena one of you told me, "This will probably be the last time I go to the beach for the next 9 months." I really hope this isn't the case. One of the most important things I want you learn in this class, besides the virial theorem and radiative transfer, is how to introduce balance in your lives. Your success as scientists depends on it. 

If you feel like you can't get back to the beach sometime in the next month, please come talk to me or Jackie. We're both extremely busy, with teaching, our research, taking classes, etc. However, one of the reasons Jackie and I have made it to this point in our careers is that we have aspects of our lives that compete with astronomy for our time, and we often let those non-astronomy things win. We'd like to help you out if you need it.

Right now, I have a paper I need to write. However, my son's soccer game is competing for my time. This morning, soccer is going to win.

Here are some pics from Lab 1. I wish I took more. Let me know if you have any that you'd like to share.